DSC 40B

Problem #013

Tags: asymptotic notation

Let $f(n) = \displaystyle\frac{n^3 - 2n^2 + 100}{n + 10}$ True or False: $f(n) = O(n^4)$

True False

Solution

True.

Problem #014

Tags: asymptotic notation

Suppose $f(n) = \Omega(n^3)$ and $g(n) = \Omega(n)$.

True or False: it is necessarily the case that $f/g = \Omega(n^2)$.

True False

Solution

False.

Problem #015

Tags: asymptotic notation

Let $f(n) = n \cdot(\sin{n} + 1 )$. A plot of this function is shown below.

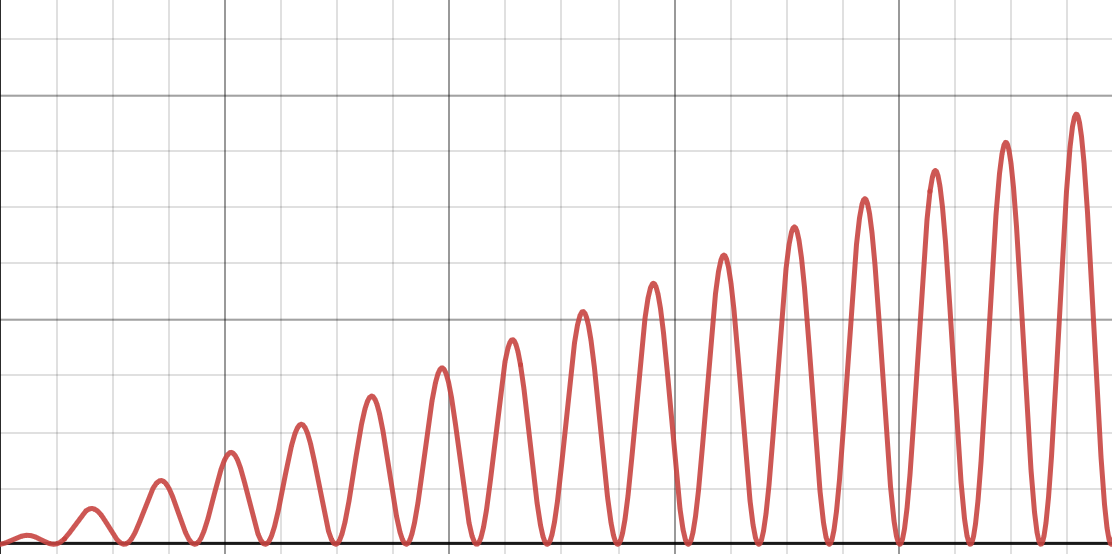
True or False: $f(n) = \Theta(n)$.

True False

Solution

False.

Remember that for $f(n)$ to be $\Theta(n)$, it has to be both upper- and lower-bounded by some positive constant times $n$. This function is upper bounded by $O(n)$, but it doesn't have a lower bound of $\Omega(n)$. Therefore, it can't be $\Theta(n)$.

In other words, there is no positive constant $c$ and no positive number $N$ such that $f(n) > c n$ for all $n > N$.

If you had to describe this function in asymptotic notation, you could say that $f(n) = O(n)$(and that would be a tight upper bound), but there is no lower bound, since the function keeps coming back down to zero.

Problem #025

Tags: asymptotic notation

Let $f$ be the piecewise function defined as:

\[ f(n) = \begin{cases} 1, & \text{if $n$ is a multiple of 1 million},\\ n^2, &\text{otherwise}. \end{cases}\]

If you were to plot $f$, the function would look like $n^2$, but would have point discontinuities where it ``jumps'' back to 1 whenever $n$ is a multiple of 1 million.

True or False: $f(n) = \Theta(n^2)$.

True False

Solution

False.

$f(n)$is upper bounded by $O(n^2)$, but it doesn't have a lower bound of $\Omega(n^2)$, which is necessary for it to be $\Theta(n^2)$.

To see why, remember that for $f(n)$ to be $\Omega(n^2)$, there must be a positive constant $c$ so that $f(n)$ stays above $c\cdot n^2$ for all $n$ greater than some $n_0$, meaning that it goes above $c n^2$and it stays above $c n^2$ forever, after some point.

Pick whatever positive $c$ you'd like -- the function $c\cdot n^2$ grows larger and larger as $n$ increases, and eventually becomes larger than 1. But the function $f(n)$ keeps dipping down to 1, meaning that it doesn't stay above $c\cdot n^2$ for all $n$ when $n$ is large. Therefore, $f(n)$ is not $\Omega(n^2)$, and therefore also not $\Theta(n^2)$.

Problem #026

Tags: asymptotic notation

Suppose $f(n)$ is both $O(n^2)$ and $\Omega(n)$, and suppose $g(n) = \Theta(n^3)$. What are the tightest possible asymptotic bounds that can be placed on $f + g$?

If the upper and lower bounds are the same, you may use $\Theta$. If the upper and lower bounds are different, you should state them separately using $O$ and $\Omega$.

Solution

$\Theta(n^3)$

Problem #029

Tags: asymptotic notation

Consider the function $f(n) = \frac{n^8 + 2^{3 + \log n} - \sqrt n}{20 n^5 - n^2}$.

True or False: $f(n) = O(n^{4})$.

True False

Solution

True.

Problem #031

Tags: asymptotic notation

Suppose $f_1(n) = O(g_1(n))$ and $f_2(n) = \Omega(g_2(n))$. True or False: it is necessarily the case that $f_1 + f_2 = O(g_1(n))$.

True False

Solution

False.

Problem #033

Tags: asymptotic notation

Let $f$ and $g$ be as in the previous question. What are the tightest possible asymptotic bounds that can be placed on the product, $f \times g$?

As before, if the upper and lower bounds are the same, you may use $\Theta$; otherwise you should use $O$ and $\Omega$.

Solution

$O(n^5)$ and $\Omega(n^4)$

Problem #043

Tags: asymptotic notation

Consider the function $f(n) = \frac{n^8 + 2^{3 + \log n} - \sqrt n}{20 n^5 - n^2}$.

True or False: $f(n) = \Omega(n^2)$.

True False

Solution

True.

Problem #045

Tags: asymptotic notation

Suppose Algorithm A takes $\Theta(n^2)$ time, while Algorithm B takes $\Theta(2^n)$ time. True or False: there could exist an input on which Algorithm $B$ takes less time than Algorithm A.

True False

Solution

True.

Problem #046

Tags: asymptotic notation

Let

\[ f(n) = \frac{n^3 - 2n + 100}{\sqrt n}\cdot\frac{n}{n^3 + n^2 + \sin n}\cdot n^2 \]

True or False: $f(n) = \Theta(n^2)$.

True False

Solution

False.

Problem #054

Tags: asymptotic notation

Consider the function $f(n) = n \times(\sin(n) + 1)$. A plot of this function is shown below:

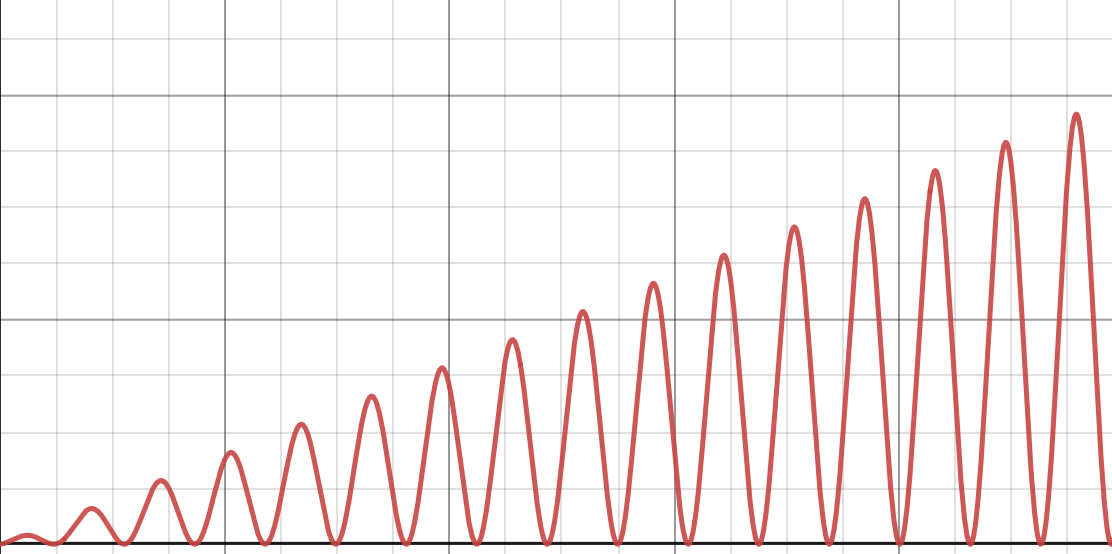
True or False: this function is $O(1 + \sin n)$.

True False

Solution

False.

$f(n)$ grows arbitrarily large, while $\sin n + 1$ is bounded above by 2.

More formally, there is no constant $c$ such that $c (1 + \sin n)$ upper bounds $f(n)$ for all large $n$.

Problem #057

Tags: asymptotic notation

Suppose $f_1(n)$ is $O(n^2)$ and $\Omega(n)$. Also suppose that $f_2(n) = \Theta(n^2)$.

Consider the function $g(n) = f_2(n) / f_1(n)$. True or false: it must be the case that $g(n) = \Omega(n)$.

True False

Solution

False.

Problem #058

Tags: asymptotic notation

Suppose $f_1(n) = \Omega(g_1(n))$ and $f_2 = \Omega(g_2(n))$. Define $f(n) = \min\{ f_1(n), f_2(n) \}$ and $g(n) = \min\{ g_1(n), g_2(n)\}$.

True or false: it is necessarily the case that $f(n) = \Omega(g(n))$.

True False

Solution

True.

Problem #060

Tags: asymptotic notation

Consider again the function $f(n) = n \times( \sin(n) + 1)$ from the previous problem.

True or False: $f(n) = O(n^3)$.

True False

Solution

True.

Problem #070

Tags: asymptotic notation

Suppose $f_1(n)$ is $O(n^2)$ and $\Omega(n)$. Also suppose that $f_2(n) = \Theta(n^2)$.

Consider the function $f(n) = f_1(n) + f_2(n)$. True or false: it must be the case that $f(n) = \Theta(n^2)$.

True False

Solution

True.

Problem #073

Tags: asymptotic notation

Let

\[ f(n) = 5 n \log n + \frac{n^3 + 5}{n + 2 + |\sin \pi n|} + n \sqrt n \]

Write $f$ in asymptotic notation in as simplest terms possible.

Solution

$f(n) = \Theta(n^2)$

Problem #091

Tags: asymptotic notation

Suppose $f_1(n) = O(g_1(n))$ and $f_2 = O(g_2(n))$. Define $f(n) = \min\{ f_1(n), f_2(n) \}$ and $g(n) = \min\{ g_1(n), g_2(n) \}$. True or false, it is necessarily the case that $f(n) = O(g(n))$.

True False

Solution

True.

Problem #093

Tags: asymptotic notation

Suppose $f(n) = \Omega(n^3)$ and $g(n) = \Omega(n)$.

True or False: it is necessarily the case that $f/g = \Omega(n^2)$.

True False

Solution

False.

Problem #171

Tags: asymptotic notation

Suppose $f_1(n)$ is $O(n^3)$ and $\Omega(n)$. Also suppose that $f_2(n) = O(n^2)$ and $\Omega(\sqrt n)$.

Consider the function $f(n) = f_1(n) + f_2(n)$. True or false: it must be the case that $f(n) = \Omega(n)$.

True False

Solution

True

Problem #172

Tags: asymptotic notation

Consider the function $f(n) = \sin(12 n) \cdot\cos(n) + 2$. A plot of this function is shown below:

True or False: this function is $\Theta(1)$.

True False

Solution

True. This function is upper bounded by 3 and lower bounded by 1 for all $n$, and is therefore $\Theta(1)$.

Problem #173

Tags: asymptotic notation

Consider again the function $f(n) = \sin(12n) \cdot\cos(n) + 2$ from the previous problem.

True or False: $f(n) = O(n^3)$.

True False

Solution

True. We saw that this function is $\Theta(1)$, but it is also correct to say that it is $O(n^3)$, though this is not a tight upper bound.

Problem #184

Tags: asymptotic notation

Suppose $f_1(n) = \Omega(g_1(n))$ and $f_2 = \Omega(g_2(n))$. Define $f(n) = \max\{ f_1(n), f_2(n) \}$ and $g(n) = \max\{ g_1(n), g_2(n)\}$.

True or false: it is necessarily the case that $f(n) = \Omega(g(n))$. In other words, it must be the case that $\max\{ f_1(n), f_2(n) \} = \Omega( \max\{ g_1(n), g_2(n) \}) $

True False

Solution

True

Problem #185

Tags: asymptotic notation

Suppose again that $f_1(n)$ is $O(n^3)$ and $\Omega(n)$. Also suppose that $f_2(n) = O(n^2)$ and $\Omega(\sqrt n)$.

Consider the function $g(n) = f_2(n) / f_1(n)$. Give the tightest possible upper bound on $g(n)$:

$O($ $n$ $)$

Problem #187

Tags: asymptotic notation

Let

\[ f(n) = \frac{n^3 + 10 n}{\sqrt{n} - 100}\times\frac{ \log(n^2 + 10)}{n(n+1)}\]

Write $f(n)$ in asymptotic notation in the simplest terms possible.

$f(n) = \Theta($ $\sqrt n \log n$ )

Problem #195

Tags: asymptotic notation

Suppose again that $f_1(n)$ is $O(n^3)$ and $\Omega(n^2)$. Also suppose that $f_2(n)$ is $O(n^4)$ and $\Omega(n)$.

Consider the function $g(n) = f_2(n) / f_1(n)$. Give the tightest possible upper bound on $g(n)$:

$O($ $n^2$ $)$

Problem #198

Tags: asymptotic notation

Suppose $f_1(n)$ is $O(n^3)$ and $\Omega(n^2)$. Also suppose that $f_2(n)$ is $O(n^4)$ and $\Omega(n)$.

Consider the function $f(n) = f_1(n) + f_2(n)$. True or false: it must be the case that $f(n) = \Omega(n^2)$.

True False

Solution

True

Problem #205

Tags: asymptotic notation

Let $f(n) = 3n^2 \log n$. True or False: $f(n) = O(n^3)$.

True False

Solution

True

Problem #207

Tags: asymptotic notation

Let

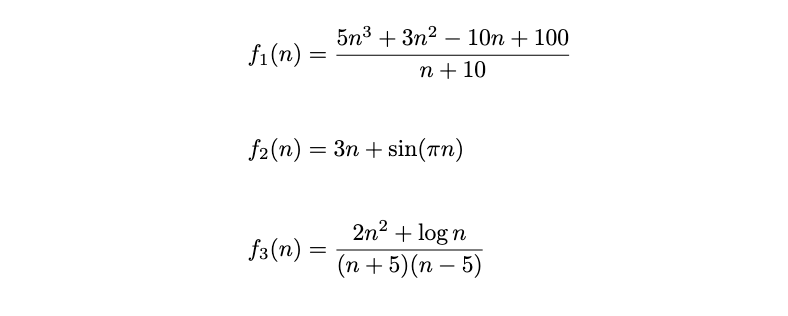
Define $f(n) = f_1(n) \times f_2(n) \times f_3(n)$. What is $f(n)$, in asymptotic notation, in simplest terms possible?

$\Theta(n^3)$

Problem #208

Tags: asymptotic notation

Consider the function defined below:

\[ f(n) = \begin{cases} 3n, & \text{if $n$ is even;}\\ 5n ,& \text{if $n$ is odd.} \end{cases}\]

True or False: $f(n) = \Theta(n)$.

True False

Solution

True

DSC 40B – Theoretical Foundations of Data Science II

Problems tagged with "asymptotic notation"

Problem #013

Problem #014

Problem #015

Problem #025

Problem #026

Problem #029

Problem #031

Problem #033

Problem #043

Problem #045

Problem #046

Problem #054

Problem #057

Problem #058

Problem #060

Problem #070

Problem #073

Problem #091

Problem #093

Problem #171

Problem #172

Problem #173

Problem #184

Problem #185

Problem #187

Problem #195

Problem #198

Problem #205

Problem #207

Problem #208